СОРОСОВСКИЕ ОЛИМПИАДЫ

Плюсы и минусы официальных советских олимпиад школьников

Зачем нужно было придумывать новый тип олимпиад для школьников? Разве традиционные олимпиады не решали задачи определения наиболее талантливых из них? Ответ на этот вопрос требует довольно длинного объяснения, но я хочу предварить его одним личным замечанием. Со школьных лет у меня всегда было уважение к олимпиадам как к таковым. Появившиеся около 50 лет тому назад в СССР школьные олимпиады в начальном своем периоде играли роль турнира для всех талантливых учеников, хотя участников из сел и деревень было неизмеримо меньше, чем из крупных городов.

Сначала школьники соревновались лишь по физике и математике, потом идея привилась, и круг дисциплин, по которым стали проводить олимпиады, все расширялся и расширялся, захватив уже не только точные науки, но и информатику, и дисциплины гуманитарного круга.

Конечно, большинство из тех, кто проводит официальные государственные олимпиады, заслуживают искренней благодарности. Эти олимпиады продолжали и продолжают играть важную роль в поиске и отборе талантливых  детей. Из участников и  победителей олимпиад выросло много выдающихся преподавателей и ученых.

Но, наряду с успехами постепенно все отчетливее стали проявляться и очевидные недостатки. Например, год за годом олимпиадное движение трансформировалось во все более закрытое и «заорганизованное» действо взрослых вокруг талантливых детишек. Личное участие школьников стало обрастать командными первенствами школ, районов, областей, республик. Официальные олимпиады превратились в мероприятия государственного значения, в запланированные турниры. Олимпиады полностью зависели финансово от отчислений из бюджета народного образования. Сформировалась устойчивая среда так называемых олимпиадных деятелей. Кое-кто из этих деятелей ведали, именно ведали, поездками отобранных команд на  заграничные первенства и использовали олимпиады как предлог для собственной занятости и порой собственного удовольствия.

Будучи приглашенным на Всемирную Математическую олимпиаду школьников в Аргентине, я с далеким от почтения чувством услышал насмешливый (и брезгливый) рассказ одного из многолетних руководителей Всемирных олимпиад о даме, которая, по его словам, много лет подряд, сопровождая советскую команду школьников в поездках на эти олимпиады, использовала каждую из поездок для покупки, как он выразился, «пальто и шуб».

Нередко эти «лидеры» олимпиад группировались в соперничающие кланы, со всей отсюда вытекающей административной суетой и вредом для самого смысла олимпиад. Другим отрицательным моментом стал принцип административно-территориальной иерархии. Из дела, открытого для каждого, кто готов и хочет померяться силами в соревнованиях, олимпиады превратились в командные первенства школ, районов, городов, областей, республик, страны в целом. Этим был завершен отход от первоначальных идей свободного и равноправного участия в олимпиадах всех желающих. Нельзя пройти и мимо того, что сложилась практика, при которой членов команд предварительно тренируют на решение сверхзадач.

Отрицательные моменты обострились с тех пор, как российские официальные команды начали участвовать в международных олимпиадах, когда финансирование команд и контроль за их подготовкой зависят всецело от министерских или межправительственных возможностей, а победы используются в политических целях. В перестроечные времена положение ухудшилось еще более: настоящим бичом стало платное участие в олимпиадах. Плата — притом вовсе не символическая (особенно для участников финальных туров) — была повсеместной. И хотя во многих случаях организаторам олимпиад удавалось находить спонсоров, случаи, когда от участия искусственно отчуждали детей из обедневших семей, потерявших доступ к высшим ступеням олимпиад, были не единичными. Известно также, что не раз сильные команды не могли принять участие в финальных соревнованиях из-за чисто материальных причин.

Естественным образом менялись и подходы к составлению и отбору задач для олимпиад. Концептуальная сторона задач изменилась. Вместо того, чтобы основывать их только  на материале школьных программ, не уходя ни на йоту от школьных учебников, составители задач стали все старательнее биться над тем, чтобы конструировать задачи, заковыристые не только по смыслу, но и по фактическому наполнению. В один из моих приездов в Москву два руководителя олимпиад России пригласили меня вечером побеседовать и принялись уговаривать поддержать финансово их олимпиаду, аргументируя это следующим способом:

— Ни у кого в активе нет таких композиторов задач, как у нас. Мы научились делать такие задачки, что далеко не каждый профессор сможет их правильно решить.

Тем вечером я особенно ясно понял, что если создавать новую олимпиаду, то надо сделать все возможное, чтобы задачи вытекали исключительно из материала школьных программ и были посильны большинству нормально успевающих учеников.

Отодвинулась в государственных и существующих международных олимпиадах на задний план еще одна важная составляющая: вовлечение в олимпиады школьников из малых городов, поселков, сел и деревень. Нищавшие сельские школы и далекие от центров учителя-подвижники (какими в большинстве своем были и остаются учителя в глубинке) не имеют возможностей дать своим ученикам всё необходимое для того, чтобы участвовать в олимпиадах высоких уровней, наравне с лучшими школьниками из крупных городов.

Таким образом, вместо широкой и многоплановой помощи образованию в целом, олимпиады стали мероприятиями по подготовке отдельных талантливых личностей, которые бы не просто проявляли и развивали свои способности, но в угоду местным или даже государственным амбициям добывали награды, премии и  занимали престижные места.

Соросовская Олимпиада школьников

 

Сказанного достаточно для того, чтобы объяснить, почему, обдумывая возможные направления будущей Образовательной Программы, я предложил Джорджу Соросу включить в её планы проведение нового типа олимпиад школьников, которые представляли  бы собой открытый для всех конкурс и при этом исключить влияние на олимпиады руководителей или чиновников любого ранга. Я предложил постараться с самого начала максимально вовлечь в нее учителей средней школы к участию в нашей олимпиаде. Мне также казалось важным втянуть в орбиту олимпиад родителей тех учащихся, кто захочет  принять в них участие.

Эти цели  сама собой вели к новой структуре олимпиад. Вместо формирования команд нарастающего престижа (класса, школы, района, города, республики, страны) надо было создать условия, при которых никто никого не должен был группировать, мобилизовывать и подталкивать. Каждый, кто хочет, мог включиться в решение задач, никого не спрашивая и никому не докладываясь.

Чтобы претворить этот принцип Открытого Общества в жизнь, я предложил Правлению нашей Программы начать Олимпиаду  с заочного тура по переписке, на что Правление согласилось (см статьи: В. Н. Сойфер. «Международная Соросовская Программа Образования. Часть 3. Результаты специализированных программ в первый год работы», Соросовский Образовательный Журн ал, 1996, № 2, стр. 8–11; его же «Новые принципы Соросовских олимпиад школьников», там же, 1997, № 1, стр. 4–8 и статью В. Сагидова «Олимпиада школьников», там же, 1996, № 2, стр. 3).

Такие олимпиады были организованы во всех четырех странах, где была развернута Программа — в России, Украине, Белоруссии и Грузии.

Забегая вперед отмечу, что идея Соросовских Олимпиад была встречена с настороженностью многими деятелями существовавшего олимпиадного движения. Некоторые из них решили, что их монополии пришел конец, и восстали против Соросовских Олимпиад, писали письма протестов против нашего начинания, вовлекая в борьбу с нами или пытаясь вовлечь многих из педагогов. Один из руководителей Московского  физико-технического института направил письмо протеста тогдашнему вице-премьеру Российского Правительства Ю. Ф. Ярову, и только вмешательство ректора этого института Н. В. Карлова, члена нашего Правления, помогло устранить ненужные трудности. Тем не менее кое в чем наши критики даже преуспели, уговорив, например, группу педагогов напечатать в журнале «Математика в школе» призыв бойкотировать Соросовские Олимпиады и вообще протестовать против нашего начинания. В их заявлении было сказано:

«Опубликованная в прессе Соросовская программа в области точных наук, вопреки декларированным в программе Фонда общим целям, объективно направлена не на поддержку национальной Российской олимпиады, а на замену ее так называемыми Соросовскими школьными олимпиадами. Это противоречит национальным интересам России и с неизбежностью в случае реализации этой программы приведет к развалу существующей ныне системы работы с одаренными школьниками... Мы призываем научную и педагогическую общественность,  органы образования России занять в этом вопросе принципиальную позицию и не дать разрушить традиции...» («Математика в школе», 1994, № 6).

Слава Богу, никто этим горячим призывам не внял. Но мы договорились на заседании Правления, что из нашего бюджета мы поддержим и существующие в стране олимпиады, которые терпели бедствие из-за финансовых трудностей. Мы объявили в газетах, что согласны в первый год помочь тем существующим олимпиадам, которые положительно зарекомендовали себя в России. Из 400 тысяч долларов, которые мы израсходовали с сентября 1994 по сентябрь 1995 года на проведение Первой олимпиады, около четверти ушло на поддержку традиционных российских олимпиад. Масштаб выделенных нами средств был больше тех денег, которые эти олимпиады получили от российского Министерства образования.

Другое недовольство нашими действиями было связано с публикацией в газетах задач и призывами присылать нам решения по почте. Это новшество встретило массово негативное отношение «олимпиадников». «Как же так, — говорили они, — при таком подходе каждый может попросить соседа решить за него задачи, а как вы потом разберетесь, кто решил сам, а у кого «папа силен в математике»? Это же профанация олимпиад, а не открытие ворот для всех желающих!»

Однако мы понимали, что если друзья или родственники помогли тому или иному школьнику, его участие будило мысль у того, кто решил помериться силами.

Принципы проведения Соросовских Олимпиад

Основные принципы нашей Олимпиады, которые сделали ее отличной от существовавших до сих пор олимпиад, свелись к следующим:

— мы постарались придать олимпиадному движению широту, демократичность, открытость для всех учащихся, максимально подключить семью к их участию в Соросовской Олимпиаде;

— была поставлена цель создать задачи такой сложности, которые бы не выходили за рамки существующих учебных программ средней школы;

— было решено организовать сначала заочный тур, и для его проведения публиковать задачи в газетах; постараться дополнительно распространить широко задачи через школы, чтобы любой школьник мог по своему желанию принять участие в заочном туре;

— мы постарались привлечь к проверке присланных решений большое число учителей средней школы;

— тех, кто ответил правильно на большинство вопросов задач заочного тура олимпиады, было решено пригласить к участию во втором, уже очном туре, одновременно предоставив право любому учителю средней школы рекомендовать своим лучшим ученикам принять участие во втором туре наравне с победителями заочного тура (иными словами, максимально широко открыть двери всем, кто хочет участвовать в Соросовских Олимпиадах);

— победителей второго (очного) тура пригласить участвовать в заключительном туре Соросовской Олимпиады, который проводить одновременно в нескольких крупных городах страны.

Задачи нового типа

Существеными факторами, определившими успех Соросовских Олимпиад, стали принципы построения задач для нашей олимпиады:

— уйти от сложившегося «заумного» стиля, языка и содержания задач традиционных государственных олимпиад: не вносить в задачи ничего намеренно усложненного, не протаскивать никаких потаенных мыслей между строками, не подлавлвать школьника на пустячке, стараться подставить ему ножку;

— сделать ясной связь задач со школьными программами и учебниками, иными словами, все до одной задачи должны были содержать материал только из школьных программ и учебников, задачи должны были будить желение участвовать в олимпиаде, а не отталкивать сложностью, заумностью и адресованностью натасканным на такие трюки «гениям», а не обычным школьникам;

— подчеркивать в задачах, где только можно, те моменты, которые бы указывали на связь материала школьных программ и учебников с сегодняшними результатами науки и тем самым делали бы для школьников ясной важность изучения тех «азов» научного знания, без которых не может обходиться самая современная научная деятельность;

— комбинировать в каждом туре задачи, посильные любому успевающему школьнику или школьнице с задачами повышенной трудности, которые были в состоянии решить только те, кто глубоко и самобытно думает и умеет применять школьные знания на практике.

Эти условия были доведены до всех, кто конструировал задачи для нашей олимпиады.

Перед проведением каждого тура в дирекцию Программы приглашали лучших экспертов по разным дисциплинам, которые просматривали все полученные задачи и придирчиво отбирали для каждого тура наиболее яркие и качественные. Мы исходили из того, чтобы каждый способный и сообразительный школьник, без лени осваивающий школьную программу, даже если он не решил ту или иную задачу, ощутил принципиальную возможность того, что он был в состоянии решить ее.

Благодаря этому был достигнут важный социальный и личностный результат: не было случаев, когда участники любого тура по его окончании чувствовали себя неловко, обиженно, ведь у каждого хоть что-то да получалось, а, кроме того, достигалось приобщение всех учащихся к усвоению материала школьной программы и к уяснению  связи его с современной наукой.

Как эти новшества были восприняты школьниками характеризует запись, сделанная одним из участниов второго тура: «Я, наверное, не получу никакого приза, но спасибо за попытку помочь мне стать умнее». Надо заметить, что сходные мысли высказали многие из участников, об этом же нам писали и говорили на Соросовских конференциях учителя средних школ.

Вместе с тем во втором и третьем турах появились задачи повышенной сложности, что позволило выделить школьников, которые мыслят самобытно, умеют найти нестандартные отвекты на вопросы, создать свой, интересный метод решения задач. За такую самобытность добавлялись дополнительные баллы. Задачи повышенной сложности создали асы российских олимпиад и лучшие преподаватели вузов и учителя школ. Как писал известный композитор задач для олимпиад И.Ф. Шарыгин: «Один математик, ознакомившись с вариантами Соросовской олимпиады [ по математике — В.С. ], заметил, что к этой олимпиаде легко готовить школьников. Надо только (!) их лучше учить. А это позволяет нам считать, что основная наша цель — продемонстрировать возможности школьной, учебной математики — достигнута».

Каждый год росло число создаваемых для нашей олимпиады задач. За все годы было отобрано 1585 задач. Наибольшее их число, признанных учительским сообществом лучшими, было создано композиторами задач с мировым именем: математиками — И. Ф. Шарыгиным, Н. Б. Васильевым, А. А. Егоровым и А. В. Спиваком; физиком — А. Р. Зильберманом; химиками — В. В. Ереминым и С. Е. Семеновым; биологами — М. Б. Беркинблитом, С. М. Глаголевым, А. В. Жердевым, и А. А. Мартьяновым.

Руководители Соросовских Олимпиад

Организацию Соросовской Олимпиады в первые два года взял на себя учитель средней школы — математик Александр Васильевич Денисенко. Помимо чисто организационных задач, ему пришлось столкнуться и с противостоянием лидеров официальных олимпиад, которые повели настоящую борьбу против предложений о проведении заочных туров, широкой публикации задач Соросовской Олимпиады в газетах и изменения стиля и содержания задач. С весны 1996 года в российской дирекции Программы сменился руководитель Олимпиад. Денисенко вернулся к преподавательской деятельности, а его заменил Борис Иойнович Миропольский, человек с незаурядным организаторским талантом, с широким видением того, как надо взаимодействовать с учителями, с одной стороны, и с преподавателями вузов и с учеными академических институтов, с другой. Конечно, он принял от предшественника уже разросшееся и завоевавшее прочную репутацию дело. Рубикон был пройден, но Миропольский придал нашим Олимпиадам такой размах, который в первый же год его директорства далеко перекрыл результаты сразу всех предшествующих лет. 90 тысяч участников (из них почти 80 тысяч в России) — таким был численный результат Третьей олимпиады, завершившейся весной 1997 года, а во время последующих трех олимпиад общее число участников достигло 877 498 человек. Цифра по любым масштабам впечатляющая и еще вчера казавшаяся немыслимо большой: каждый десятый старшеклассник в стране померился силами в нетрадиционной, негосударственной и вообще ни для кого не обязательной Соросовской Олимпиаде.

Эта цифра означала, что идея наших олимпиад заинтересовала школьников, что нашу олимпиаду признали все, кто связан с образованием и в России, и в соседних странах. Миропольский сумел привлечь к работе по созданию задач по всем дисциплинам группу первоклассных композиторов. Без их таланта нашей Олимпиаде не удалось бы завоевать такое широкое признание.

Динамика роста количества участников

Соросовских Олимпиад

В заочном туре в первый год проведения Олимпиады приняло участие около 3 тысяч учащихся, второй тур прошел в 157 крупных городах России и собрал почти 6 тысяч участников. Третий  тур был проведен в четырех городах (Красноярске, Нижнем Новгороде, Санкт-Петербурге и Москве), и всего в этой олимпиаде участвовало 12 тысяч человек (с учетом двух тысяч школьников Белоруссии, Грузии и Украины). Во Второй Соросовской Олимпиаде в 1996 году число участников только в Российской Федерации возросло до 47 тысяч, и в трех других странах оно составило почти 23 тысячи. Финальный тур Второй Олимпиады проводили уже не в четырех, а в семи городах России: Екатеринбурге, Краснодаре, Красноярске, Нижнем Новгороде, Новосибирске, Москве и Санкт-Петербурге. Благодаря этому удалось сократить перемещения участников на значительные расстояния. Около 60% от общего числа участников приехали тогда на финальный тур из маленьких городов, поселков и деревень, что мы  рассматривали как важнейший успех. В целом, в финальном туре участвовали школьники из 602 школ, расположенных в 373 населенных пунктах.

Впервые в 1996 году Соросовская Олимпиада вышла за пределы стран, где она официально проводилась нашей Программой, так как школьники из Армении, Казахстана, Узбекистана, Латвии и Эстонии решали задачи, опубликованные в российских газетах, и присылали свои решения в Москву. Общее их число приблизилось к тысяче человек. Летом 1996 года, кроме того, была проведена первая совместная Соросовская Олимпиада учащихся Грузии, Белоруссии и Украины, отдельная от Российской Соросовской Олимпиады (она прошла в Грузии, в пригороде Тбилиси).

В ходе проведения Третьей Олимпиады в России первый (заочный) тур продолжался около двух месяцев и закончился 10 декабря 1996  года. Задачи были опублико ваны в «Учительской газете» (15 октября 1996 г.), в еженедельных предметных приложениях к газете «Первое сентября» (№ 40 и 41 за 1996 г.), в «Соросовском Образовательном Журнале» (№ 9 за 1996 г.), были распространены по  сети отдела информатизации Министерства общего и профессионального образования и по компьютерной сети Института «Информ-образование». Затем все задачи с решениями были опубликованы в специальном выпуске газеты «Первое сентября» в самом конце 1996 года (в № 47), и весь тираж (более 30 тысяч экземпляров) был разослан по всем средним школам страны, в которых есть старшие классы, а также во многие школы стран так называемого ближнего зарубежья. Благодаря этому в заочном туре приняло участие 12 264 школьника из 2750 школ, проживавших в 1360 городах  76 республик, краев и областей России и городов сопредельных стран.

Второй тур Третьей Олимпиады проходил в городах России, расположенных более или менее равномерно по всем географическим зонам страны. В нем приняло участие уже около 68 тысяч учащихся, в основном из России, а также из многих стран бывшего Советского Союза.

Огромную роль в успехе этого тура сыграли учителя и родители. Благодаря этому невиданное в мировой истории олимпиад число участников собралось на второй тур. На третий тур, проходивший в 17 городах России, 6 городах Украины и столицах Армении и Молдавии, были приглашены  победители второго тура —около 4000 учащихся. Среди них были школьники не только из России, но из Украины, прибалтийских стран, Молдавии, Киргизии, Грузии, Белоруссии и Армении. Помимо этого свои независимые Соросовские Олимпиады были проведены в Украине, Белоруссии и Грузии.

В 1998 году в Четвертой Соросовской Олимпиаде приняло участие более четверти миллиона школьников. Мелькание цифр может у томить читателя, но как без цифр можно рассказать о размахе Соросовских Олимпиад? Год от года цифра школьников, участвовавших во всех турах, нарастала лавинообразно. Например, в первом (заочном) туре во всех шести Соросовских Олимпиадах приняли участие 83 651 школьник из 3500 школ, расположенных в 1400 населенных пунктах России и тринадцати стран-соседей России — Украины, Беларуси, Молдавии, Казахстана, Киргизии, Грузии, Армении, Азербайджана, Эстонии, Литвы, Латвии, Узбекистана и Болгарии. Только в этих странах 5664 школьника решали задачи заочного тура. Они прислали свои решения в Москву. Второй тур, как всегда, был очным, и в нем также число участников значительно выросло.

Для того, чтобы создать равные условия для всех школьников по стране и за рубежом, начиная с 1997 года, его одновременно проводили в один день в школах, расположенных в девяти странах. Для этого пришлось собирать участников в 1930 школах в 1056 населенных пунктах России и сопредельных стран. Во втором туре приняли участие 30 285 школьников из соседних с Россией стран. Всего за шесть лет во всех Соросовских Олимпиадах во втором туре и в России и за рубежом состязались 766 826 учащихся.

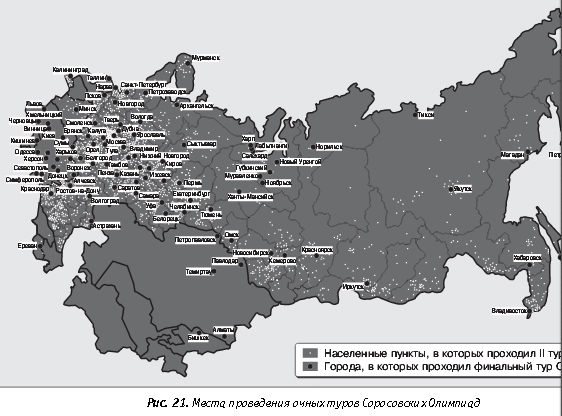
Те, кто решил наибольшее число задач во втором туре или проявил особую смекалку в ответах на какие-то определенные задачи, были приглашены на третий (заключительный) тур. Общая цифра участников третьего тура всех шести олимпиад достигла 27 021 человек. Финальный тур проводили каждый год в мае и, начиная с 1997 года, он шел в 90 городах России и сопредельных стран (рис. 1).

Мы оплачивали проезд победителей второго тура и сопровождающих их учителей в те города, где проходил третий тур, кормили всех приехавших, организовывали встречи с ведущими учеными, во многих местах в конце олимпиады для участников устраивали концерты. Именно поэтому само участие в финальном состязании, поездки в города, где проходил третий тур, стали яркими событиями в жизни 27 тысяч школьников, они запомнили на всю жизнь, как они принимали участие в завершающем этапе Олимпиад, связанных с именем Джорджа Сороса.

Победу в Соросовских Олимпиадах завоевали 2156 школьников из 79 регионов России и восьми других стран. Значительно большая группа школьников получила Дипломы Соросовской Олимпиады за успешное участие в Олимпиаде. А во всех трех турах всех олимпиад участвовало более 877 тысяч учащихся!  На графике (рис. 2) показана динамика числа участников всех олимпиад.

Роль учителей в проведении олимпиад

Конечно, при таком массовом участии школьников олимпиады нельзя было провести без помощи директоров множества школ и тысяч учителей, совершенно бескорыстно и самоотверженно уделявших немалое время для помощи как совим ученикам, так и организаторам Соросовской Олимпиады на местах. Без их участия деятельность такого масштаба была бы невозможна, наша затея попросту бы провалились. Поэтому именно фактом широкого участия директоров школ и учителей можно доказать, что идеалы Соросовской Образовательной Программы были восприняты благожелательно огромной учительской массой.

Приведу краткий список наиболее активных наших коллег, помогавших в самом начале развития Соросовского олимпиадного движения:

М. Х. Ачмиз                         Гимназия № 23, Краснодар

А. И. Кроткий,  Д. И. Уткин          Студенческий учебно-научный центр

Уральского госуниверситета (СУНЦ УрГУ),

Екатеринбург

В. Г. Косьяненко                              Школа-гимназия № 42, Новосибирск

О. Ф. Крыжановский                      Физ.-мат. лицей № 27, Харьков

П.И. Ларина                         Школа № 41, Красноярск

А. В. Лисицын                                 Вологодский государственный естественно-

математический лицей, Вологда

И. Л. Окштейн                                 Станция юных натуралистов, Москва

С. Е. Рукшин,  М. Я. Пратусевич Школа № 239, Санкт-Петербург

С. Е. Семенов                                   Химический колледж, Москва

В. И. Шелест                                    Школа № 130, Новосибирск

Р. Н. Шилков, Д. А. Эренкранц Лицей № 40, Нижний Новгород

По окончании Первой Соросовской Олимпиады Белоруссии председатель Белорусского наблюдательного Совета Программы академик Л. В. Хотылева вручает подарок одному из победителей олимпиады. Ложесно, Белоруссия, 1995 г.

Нас особенно радовало то, что свою лепту в организацию всех туров олимпиады внесли не только те, кто носят звание Соросовский Учитель, но и многие другие учителя. Я лично думаю, что это одно из самых важных свидетельств того, насколько глубоко Соросовская Программа вошла в жизнь российской школы. Палкой на такого рода мероприятие детей не загонишь, пряников там тоже не раздавали и никого никакими посулами не заманивали. И конечно, просто возможностью получить в будущем приз (при довольно малом числе их, к тому же по стоимости небольшим) такую массовость не объяснить. Мне кажется, что весь настрой Соросовских Олимпиад, дававших каждому равные права, отсутствие видимой всегда и всем поддержки кого-то из «близких» и предпочтения кому-то (причем всегда в ущерб другому) и привели к такому результату. Кстати, во время нескольких встреч с учителями на конференциях Соросовских Учителей и Профессоров мне пришлось не раз слышать слова об исключительной важности наших олимпиад, просьб о том, чтобы они продолжились и в последующем, чтобы задачи их стали доступными учителям в повседневной жизни.

Большую роль в успехе олимпиад сыграло то обстоятельство, что учителя увидели новинку: их неизменно с радушием встречали на втором и третьем турах. А ведь в проводимых под эгидой государства официальных олимпиадах двери залов всегда закрывали перед учителями — не ровен час глазами подскажут своим, как решать задачи. Мы от этой практики с самого начала резко отошли, посчитав, что участие в олимпиадах и победы в них — это совместное достижение учителя и питомца. Не следует преуменьшать и роль родителей в этой массовости.

В целом благодаря сочетанию перечисленных факторов стало возможным то, что невиданное в мировой истории олимпиад число участников собиралось на Соросовские Олимпиады.

По результатам каждой олимпиады были выявлены те школы, из которых пришло больше всего письменных решений задач первого тура, а затем школы, в которых был проведен второй (очный) тур. Более чем 1600 российским школам был выдан специальный грант за активное участие в олимпиадах. Надо особо подчеркнуть, что мы заранее не афишировали, что те школы, которые будут наиболее активны в помощи проведению Соросовской Олимпиады, получат денежные гранты. Тем более радостным для директоров и учителей этих школ было известие о присуждении им гранта. Конечно, бухгалтерам Программы добавилось работы с проверкой, на какие нужды школы потратили полученные деньги, но мы следили за тем, наградили ли директора школ тех учителей, которые нам помогали. Именно этот придирчивый контроль рождал еще больше уважения к организаторам олимпиад. Все видели, что сотрудники Соросовской Программы не сорят деньгами Джорджа Сороса, скрупулезно следят за расходованием каждого доллара и заботятся о каждом учителе, включившемся в наше дело.

Создание компьютерной базы  Соросовских Олимпиад

Конечно, затеянное дело оказалось технически довольно сложным. Надо было научиться самим оперировать с сотнями тысяч тетрадей, найти учителей и преподавателей вузов, которые бы однотипно проверили все решения. Данные проверок надо было ввести в базы компьютеров, полученные результаты проанализировать.

В компьютерную базу данных бфли введены сведения о каждом участнике и о том, как они решили каждую из задач заочного тура, а затем аналогичные данные о всех участниках очных туров. База позволила не только легко представить себе статистику решений, успехов отдельных школьников, решаемость каждой из предложенных задач (что важно для понимания того, как надо в будущем конструировать задачи), изучить распределение участников по стране и по отдельным областям, но главное — непредвзято выявлять наиболее сильных участников, распределить их не просто по числу решенных задач, а по числу решений тех задач, которые  наиболее трудно дались большинству школьников и школьниц.

Создание базы данных позволило с легкостью пойти еще на один шаг, чрезвычайно важный в философии Открытого Общества, которую старается превратить в реальность Джордж Сорос — довести результаты до всех участников и до каждой школы, чтобы каждый из учителей узнал, каких успехов достигли их ученики. Мы рассматривали этот шаг, эту в общем нелегкую задачу, как важнейший элемент открытости действий Программы, как способ показать каждому участнику Олимпиад, как и почему его решения были оценены так, а не иначе. К разосланным сведениям была приложена также итоговая таблица распределения числа участников, решивших то или иное число задач.

Новые принципы организации проверки задач

Нужно отметить также еще одно новшество, родившееся в ходе Соросовских Олимпиад. Оно связано с тем, как лучшим образом организовать проверку решения астрономически большого числа ответов. Было сформировано несколько команд проверяющих, с ними предварительно были оговорены условия проверок, обсуждены разные возможные варианты решений (стандартных и нестандартных), а затем каждая бригада приступала к работе, но и здесь мы внесли кардинальное новшество. Каждый член команды проверял во всех тетрадках с ответами, пришедшимися на эту команду, только какой-то один вопрос, другой проверяющий приступал к другому вопросу и так далее. Такой подход позволил резко увеличить эффективность и скорость проверки. Повторяя анализ решения одного и того же вопроса, каждый проверяющий наращивал и наращивал темпы работы и тратил все меньше и меньше времени на одну и ту же операцию. Как шутил один из моих друзей, «ничего нового вы не придумали, это был старый принцип родоначальника империи Форда, отображенный Чарли Чаплином, и назывался он конвейер». Этот подход, помимо увеличения скорости проверки, позволял каждому проверяющему легче заметить нестандартные решения и добавить за них баллы.

К тому же каждая работа оценивалась теперь одинаково у всех участников олимпиады, и личные пристрастия проверяющего отступали на задний план (теперь было неважно, как технически выполнил решения тот или иной участник или участница — аккуратно, неряшливо, таким почерком или иным — на первое место выступала творческая сторона, способ решения, его новизна,  оригинальность). Благодаря такому ускорению процесса проверки удалось уложиться с ней в срок.

Летом 1997 года я случайно столкнулся с тем, каким непривычным показался такой «конвейерный» метод многим организаторам международных олимпиад, чаще всего следовавшим противоположному подходу: не давать возможности проверяющим специализироваться на чем-то одном, а, напротив, менять местами членов команд проверяющих.

Весной 1997 года мне позвонил профессор Небрасского университета Уолтер Миентка, который много лет ведет основную работу по проведению славящейся своей массовостью математической олимпиады США, а также избирается не один десяток лет ответственным секретарем Международной Математической олимпиады. Он пригласил меня сделать доклад о принципах нашей олимпиады на заседании их Оргкомитета перед началом 38-й Международной Математической олимпиады, которая должна была состояться в Аргентине в июле 1997 года.

Первая наша встреча с Уолтером Миенткой состоялась за месяц до поездки в Аргентину во время торжественного приема в Вашингтоне по случаю окончания американской олимпиады, на котором чествовали восьмерых победителей олимпиады США этого года, причем чествование это проходило в одном из самых престижных мест столицы США — в зале приемов Госдепартамента, а поздравления восьмерке победителей поступили от Президента США Билла Клинтона и его жены (вот на каком уровне проявляют уважение к своим участникам олимпиад и их победителям американцы!).

Во время ужина Миентка сел рядом со мной, и мы быстро перешли к обсуждению деталей нашей работы. Когда в первый раз я упомянул о том, что в нашей олимпиаде в том году приняло участие 90 тысяч школьников и все они решали полноценные задачи, он промолчал, но я заметил искорку недоверия в его глазах. Второй раз, уже открыто и с оттенком не прощающей мое хлестаковство улыбкой, Уолтер высказался в самолете, когда мы летели в Аргентину. Свой скепсис он объяснил просто, ссылаясь на свой многолетний опыт в этом деле: физически невозможно в обозримо короткий срок проверить 90 тысяч полноценных решений задач, это никому не под силу. (Попутно замечу: такого числа участников, решающих настоящие задачи, не знала и не знает ни одна из олимпиад в мире. Так, в математической олимпиаде США участвует около 600 тысяч школьников, но из них только около 4 тысяч решают истинные задачи, а остальные отвечают на слабенькие тесты, вроде такого: сколько будет 2 + 2 + 2 + 2 + 2 + 2?).

Помня скепсис профессора Миентки, я решил уделить время в своем выступлении в Буэнос-Айресе на то, чтобы объяснить, как же проверяли в России решения задач у девяноста тысяч участников за срок, меньший двух месяцев, притом проверяли так, чтобы избежать казалось бы неминуемого введения разных стандартов в проверку.

После моего выступления многие члены Оргкомитета высказались по поводу принципов нашей Олимпиады, затем уже во время самой олимпиады мы несколько раз разговаривали и с Президентом Олимпиады Клодом Де Шампом и с другими членами Оргкомитета, и я понял, что все они хотят наши новшества перенести в их страны. Сейчас я знаю, что «конвейерный» метод подхватили организаторы олимпиад во многих странах, ибо он по-настоящему помогает уравнять шансы тех, кто решает задачи, и одновременно ускорить работу по проверке задач.

Прямой прием в вузы призеров Соросовских Олимпиад

Соросовские Олимпиады принесли их участникам и практическую пользу, о которой мы вначале даже и не думали. Убедившись в высоком уровне наших Олимпиад, уже в 1995 году ученые советы многих вузов приняли решение о зачислении победителей нашей олимпиады в эти вузы без экзаменов, а кое-кто, например, руководство Московского физико-технического института организовало вступительные экзамены прямо во время третьего тура. Многие школьники выпускных классов тут же сумели успешно сдать экзамены и стать студентами этого самого престижного в естественных науках вуза, еще не начав сдавать выпускные экзамены у себя  в школах.

На химическом факультете Московского государственного университета имени М.В. Ломоносова декан факультета академик В. В. Лунин распорядился провести лишь собеседования для победителей нашей олимпиады, а успешно прошедших этот тест приняли на химфак без экзаменов. В последующие годы Валерий Васильевич Лунин убедился в том, то такое нововведение полностью себя оправдало: призеры Соросовских Олимпиад не только успешно учились на первом курсе, они стали лидерами на факультете и на более старших крусах. Лунин неоднократно выступал в печати со статьями на эту тему. Вместе с представителями нашей Программы он поехад в Голландию на конгресс, организованный ЮНЕСКО, где поделился своими заключениями о важности привлечения победителей Соросовских Олимпиад в студенты своего факультета. Вернувшись из Амстердама, он прислал мне письмо от 3 октября 1997 года с подробным рассказом о том, как было встречено его выступление:

«Мои коллеги и я провели чрезвычайно полезные дискуссии с голландскими специалистами о системах образования в Голландии и России и о месте и роли олимпиад в этих системах. В частности, в нашем докладе о Соросовской Олимпиаде по химии мы отметили выдающуюся роль Соросовской Образовательной Программы в развитии инфраструктуры информационного обмена с региональными образовательными центрами России.

Голландские коллеги были потрясены масштабом Соросовской Олимпиады, которая по числу участников на порядок превосходит их национальные олимпиады. Благодаря Соросовской Программе многие тысячи школьников узнали, что химия — это чрезвычайно увлекательная и перспективная область человеческой деятельности, так как химики не только познают Природу, но и изменяют ее, создавая новые вещества и материалы.

Голландскую сторону очень заинтересовал один из побочных эффектов Соросовской Олимпиады, а именно — резкое (на одну треть!) увеличение конкурса среди поступающих на химический факультет Московского университета  (рис. 3). Мы объяснили этот результат тесным, устойчивым и плодотворным сотрудничеством химического факультета и Соросовской Образовательной Программы. Более того, во многом благодаря Вашей Программе меняется “география” вступительных экзаменов: в 1997 г. более половины первокурсников химфака (109 из 215) — жители “провинциальной” России (более 50 областей и республик)».

Несомненно, решение руководства ведущих вузов страны принимать призеров нашей олимпиады в их вузы без экзаменов показало, что Соросовские олимпиады получили высокую оценку. Воспользовались нашими олимпиадами и некоторые другие организации. Так, Колмогоровский интернат при МГУ рекрутировал в число своих воспитанников многих школьников уже на втором туре Соросовской Олимпиады. МИФИ, РХТУ (Менделеевский университет) в Москве, Нижегородский университет и многие другие вузы, куда попасть нелегко и где в последние годы снова возродился конкурс поступающих, начали принимать наших победителей без дополнительных испытаний.

В 1997 г. наблюдалось резкое увеличение числа поступивших, обусловленное, как считал автор этого графика декан химического факультета МГУ академик В. В. Лунин, приемом на факультет призеров Соросовской Олимпиады.

В последующие годы эта практика была значительно расширена. Многие ведущие  вузы России, Украины, Белоруссии и Грузии открыли свои двери для победителей Соросовских Олимпиад еще до начала конкурсных экзаменов. Произошло это вовсе не потому, что наплыв в вузы прекратился: напротив, ведь начиная с 1994 года, устойчиво наблюдался все более острый подъем интереса молодежи к поступлению в вузы, в том числе на дисциплины теоретического, а не только коммерческого профиля. В большинстве ведущих вузов конкурсы за каждое место снова стали отнюдь не символичными. В этих условиях даже придирчивым руководителям ведущих вузов, где конкуренция за студентов восстановилась, стало ясно, что победители нашей олимпиады имеют высокий уровень подготовки, что они сообразительны и сильны, поэтому дополнительная их перепроверка в ходе экзаменов или собеседований не нужна. Они поняли, как важно привлечь в ряды студентов победителей столь ответственной и высоко ценившейся олимпиады как Соросовская Олимпиада Школьников. Не скрою, мне было приятно читать слова И. Ф. Ша рыгина в сборнике задач и их решений, изданных нашей Программой:

«...сегодня... смело можно воспользоваться известной формулой: если бы Соросовских олимпиад не было, их бы следовало придумать. А потому — спасибо тем, кто их придумал» (Сборник «Соросовская Олимпиада Школьников», Москва, 1995, стр. 305).

Интерес в мире к Соросовским Олимпиадам

Не только математикам оказалось интересным узнать подробнее о Соросовской Олимпиаде. В конце 1996 года вместе с бывшим министром образования Российской Федерации профессором Е. В. Ткаченко, перешедшим на работу в дирекцию Российского отделения Соросовской Образовательной Программы, мы побывали в Париже у Генерального Директора ЮНЕСКО профессора Федерико Майора и у трех его заместителей. Я рассказывал, конечно, не только об олимпиадах, но и о всех мероприятиях Программы. Наиболее интересными Майору показались три наших новинки: опрос огромного числа студентов институтов для выявления лучших школьных учителей стран, где работает наша Программа, принципы проведения Соросовских конференций учителей и организации Соросовских Олимпиад.

Федерико Майор поручил своему сотруднику (очень кстати оказавшемуся российским гражданином, много лет работающим в этой международной организации и отвечающим в аппарате ЮНЕСКО за олимпиады) А. Н. Покровскому перенять, насколько возможно, эти новинки. С подачи Покровского Б. И. Миропольский в 1997 году выступил на заседании представителей стран-участниц Международной Химической олимпиады в Монреале. Затем меня пригласили в 1998 году на заседание Оргкомитета Международного Союза чистой и прикладной химии. В том же году группа составителей задач нашей олимпиады побывала в Голландии, где с обрались организаторы олимпиад из этой страны. В целом эти приглашения говорили о том интересе, который наша олимпиада вызвала в мире.

Успехи победителей Соросовских Олимпиад на всемирных олимпиадах

Показателем высокого уровня Соросовских Олимпиад стал тот факт, что шесть лет подряд официальные команды тех стран, где функционировала наша Программа, включали в себя почти 90% победителей Соросовских Олимпиад и что максимальное количество золотых, серебряных и бронзовых наград официальным командам принесли именно победители наших Олимпиад.

Уже в 1995 году российские команды на всемирных олимпиадах по математике (Торонто, Канада), физике (Канберра, Австралия) , химии (Пекин, Китай) и биологии (Бангкок, Таиланд)  были составлены в основном из победителей Соросовских Олимпиад. В каждой из этих олимпиад именно призеры Соросовских Олимпиад завоевали золотые и серебряные медали. В 1996 году в целом из 19 медалей, полученных российскими участниками на этих олимпиадах, 14 достались победителям Соросовских Олимпиад.

Этот замечательный результат был повторен и в последующие годы. Например, в 1999 году российские лауреаты Соросовских Олимпиад завоевали на международ ных олимпиадах 9 золотых, 4 серебряных и 5 бронзовых медалей.

Особо надо отметить то, что произошло в Грузии. В этой стране Президент Э.А. Шеварднадзе и правительство на протяжении нескольких лет поддерживали равными с Соросом деньгами нашу Программу. С 1995 года в Грузии проводили свои Соросовские Олимпиады и внимательно следили за их победителями. Бывшие лауреаты ранних Соросовских Олимпиад в Грузии, ставшие молодыми учеными, завоевали в 2000 году несколько высших наград на Европейских конкурсах. Так, они приняли участие в чрезвычайно престижном конкурсе «Молодые Ученые Европы» в Амстердаме и заняли больше призовых мест, чем представители любой другой страны Европы (пять из сорока, причем получив the Grand Prix конкурса). В 2002 году Соросовские Студенты из Грузии завоевали на 33-й Международной Физической олимпиаде две золотых, две серебряных и одну бронзовую медали. Президент Грузии Э. А. Шеварднадзе, руководители грузинского образования и интеллектуалы этой страны расценили данный результат как замечательный успех. Победа на европейском конкурсе из важного, но все-таки довольно локального события, переросла в разряд существенного государственного и политического достижения — маленькая страна Грузия заявила о себе на мировой арене важным достижением в интеллектуальной сфере.

Президент Грузии отметил в своем письме 8 августа 2002 года:

«Дорогой мистер Сорос, дорогой мистер Сойфер,

С огромным удовольствием хочу проинформировать Вас и даже более того, поздравить Вас с победой пяти членов грузинской команды студентов, которые сумели завоевать пять медалей... на олимпиаде в Индонезии...

Честь за эти достижения главным образом принадлежит Международной Соросовской Программе Образования, которая помогла учащимся школ и студентам университетов в усвоении точных наук. Это именно та причина, по которой многие грузинские студенты были приглашены учиться в ведущие иностранные университеты.

Я рад воспользоваться этой возможностью и поблагодарить Вас за Вашу работу, которая исключительно важна для настоящего и будущего Грузии.

Искренне Ваш Эдуард Шеварднадзе».

 

Издание сборников задач и решений

 

Первый сборник задач Соросовской Олимпиады и их решений был издан в Белоруссии Анатолием Александровичем Шубой («Задачи Белорусской математической олимпиады школьников 1994 г.», Минск, 1995, Изд. Института математики Академии наук Беларуси, 102 стр.).

В России аналогичный cборник появился благодаря настойчивости А. В. Денисенко. После завершения Первой Соросовской Олимпиады сборник всех задач, предложенных в 1995 году во всех турах в России, был опубликован двадцатитысячным тиражом.

Задачи, предлагавшиеся на первой Соросовской Олимпиаде в Грузии в 1996 г., были включены, наряду с задачами ряда других олимпиад, в сборник «Математические соревнования Грузии (1996/1997)», К. Цискаридзе, Тбилиси, 1997, 240 стр.).

В то время мы еще не создали компьютерный банк данных о всех средних школах России с 9–11 классами. Поэтому рассылка сборника оказалась непростой задачей. Несмотря на это, он разошелся по школам довольно быстро, и мы начали получать первые  сведения о том, что учителя старших классов полюбили его и стали использовать в повседневной учебной работе в качестве дополнительного пособия. В отзывах многих учителей средних школ говорилось о хорошем качестве задач и о полезной роли сборника. С тех пор каждый год мы публиковали новый сборник. В результате получилась библиотека новых учебников, причем многие учителя сообщали, что привлекают задач из сборников в повседневной учебе. Второй и последующие сборники вплоть до шестого готовил к выходу в свет Б. И. Миропольский. Второй и третий сборники вышли тиражом 40 тысяч экземпляров, четвертый, пятый и шестой — тиражами по 25 тысяч экземпляров. Сборники были  разосланы по всем средним школам в краткий срок, подарены всем Соросовским учителям, приобрели известность и популярность.

К читателям 3-го сборника обратился Джордж Сорос. Он писал:

 

« Рад приветствовать всех читателей этой книги. Третий раз учителя и учащиеся средних школ получают сборник задач с решениями и могут использовать их в ежедневной практике. Я хочу поблагодарить тех, кто принял участие в создании задач, опубликованных в  этой книге. Из писем, которые я получил от российских, украинских, белорусских и грузинских учителей, я узнал, что наши Олимпиады стали важной частью образовательного процесса.

Наши Олимпиады доказали их важность. Они открыты для каждого, и более 90 000 школьников приняли участие в Олимпиаде 1997 года.

На меня произвело большое впечатление сообщение о том, что победители наших Олимпиад завоевали огромное количество золотых, серебряных и бронзовых медалей на Международных Олимпиадах по физике, математике, биологии и химии. Я надеюсь, что данная книга будет полезна как учителям, так и школьникам, и вдохновит последних на более глубокое понимание новых фактов и направлений современной науки. Я желаю всем вам большого успеха в работе и в жизни.

Искренне Ваш

Джордж Сорос».